Οι Χημικοί Μηχανικοί γνωρίζουμε πολύ καλά ότι τριβή και παραγωγή εντροπίας πάνε "χέρι-χέρι"! Η τριβή συνδέεται με αναντίστρεπτες διεργασίες, που με τη σειρά τους οδηγούν στην αυθόρμητη παραγωγή εντροπίας! Αυτή η θεμελιώδη σύζευξη (2ος Θερμοδυναμικός Νόμος) έχει αποτελέσει τον θεμέλιο λίθο πάνω στον οποίο βασίστηκε η σύγχρονη ανάπτυξη της Επιστήμης της Θερμοδυναμικής Εκτός Ισορροπίας και η αυστηρή γεωμετρική της θεμελίωση. Οι ίδιες έννοιες μπορούν να χρησιμοποιηθούν για την περιγραφή της χρονικής εξέλιξης ενός δυναμικού συστήματος μέσω της διατύπωσης χρονο-μεταβαλλόμενων εξισώσεων με μια πολύ αυστηρή θερμοδυναμική δομή στην οποία αντιστρεπτές και μη αντιστρεπτές διεργασίες συνεισφέρουν είτε ξεχωριστά είτε συζευγμένα.
Αυτό όμως που δεν είναι καθόλου ευρέως γνωστό είναι πως παρόμοιες δυναμικές εξισώσεις μπορούν να θεμελιωθούν και για ανοιχτά κβαντικά συστήματα, με τις αναντίστρεπτες διεργασίες εκεί να εισάγουν μηχανισμούς εξομάλυνσης όρων στις τελικές εξισώσεις που οδηγούν σε απειρισμούς και άρα στην ανάγκη επανα-κανονικοποίησης της αντίστοιχης θεωρίας.
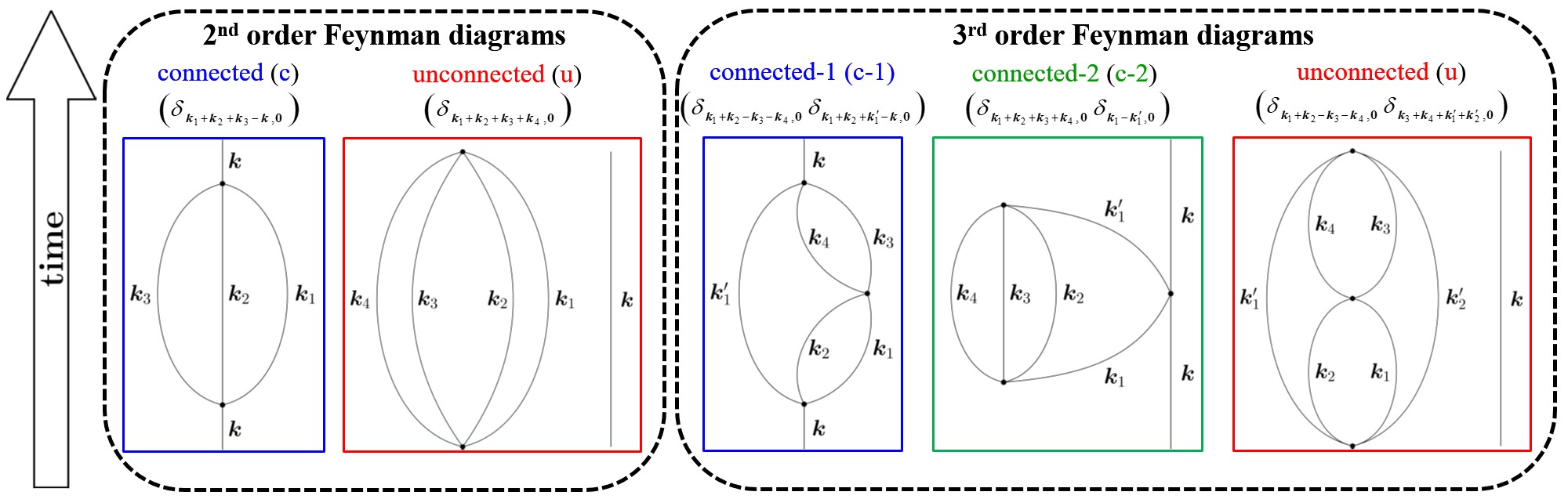
Σε μια πρόσφατη δημοσίευση στο φημισμένο επιστημονικό περιοδικό Physical Review D, ο Διδακτορικός Φοιτητής του Τμήματος Παναγιώτης Αλατάς και ο ερευνητικός του επιβλέποντας καθ. Βλάσης Μαυραντζάς από το Τμήμα μας, σε μια εξαιρετική συνεργασία με τον καθ. Hans Christian Öttinger από το Πολυτεχνείο ETH της Ζυρίχης (https://polyphys.mat.ethz.ch/group/people/head.html) παρουσιάζουν την εφαρμογή μιας τέτοιας προσέγγισης στην απλούστερη δυνατή κβαντική θεωρία, γνωστή και ως θεωρία φ^4 που περιγράφει την ταυτόχρονη αλληλεπίδραση στο χωρόχρονο 4 κβαντικών βαθμωτών σωματιδίων. Με τη βοήθεια μιας κβαντικής καταστατικής εξίσωσης από τη Θερμοδυναμική Εκτός Ισορροπίας για την χρονο-εξέλιξη ενός τέτοιου συστήματος, οι τρεις ερευνητές κατάφεραν να υπολογίσουν τα αντίστοιχα διαγράμματα Feynman μέχρι όρους 3ης τάξης ως προς την παράμετρο αλληλεπίδρασης των 4 σωματιδίων με σαφή κατεύθυνση χρόνου (αύξουσα), και να αναλύσουν την τοπολογία τους. Στη συνέχεια, παρουσιάζουν μια πολύ κομψή επιλογή των παραμέτρων της θεωρίας ώστε να αποφεύγεται η εμφάνιση απειρισμών ή ολοκληρωμάτων που δεν συγκλίνουν, και στο τέλος αποδεικνύουν πως η νέα θεωρία στο όριο που δεν υπάρχουν τριβές αναπαραγάγει πολύ όμορφα το αποτέλεσμα της γνωστής κλασσικής Λαγκρανζιανής προσέγγισης στο ίδιο πρόβλημα!
Η εργασία αναδεικνύει τις ατελείωτες προεκτάσεις εννοιών και αρχών που διδασκόμαστε στην Επιστήμη της Χημικής Μηχανικής (τριβή και εντροπία) και πως αυτές μπορούν να χρησιμοποιηθούν ώστε να περιγράψουν πολύπλοκες αλληλεπιδράσεις και μηχανισμούς, προσφέροντας μοναδικές λύσεις σε θεμελιώδη προβλήματα σε όλο το φάσμα των φυσικών-χημικών επιστημών (κλασσικών και κβαντικών)!
Περισσότερες πληροφορίες: https://journals.aps.org/prd/abstract/10.1103/PhysRevD.104.076007
| Συνημμένο | Μέγεθος |
|---|---|
| physrevd.104.076007.pdf | 565.71 KB |
