We all know that entropy and friction go hand-in-hand. Friction creates irreversibility which results in the generation of entropy. This fundamental coupling has been the cornerstone of modern equilibrium and (more importantly) nonequilibrium thermodynamics and has helped lay the geometric foundations of the latter. The same two concepts can be used to formulate time-evolution equations for nonequilibrium systems that possess a well-defined thermodynamic structure in which reversible and irreversible contributions are constructed separately. What we know less, however, is that similar time-evolution equations can be formulated for quantum systems, wherein it can be shown that irreversibility (friction) introduces a dissipative smoothing of fields thus providing ultraviolet regularization of the underlying quantum field theory (QFT).
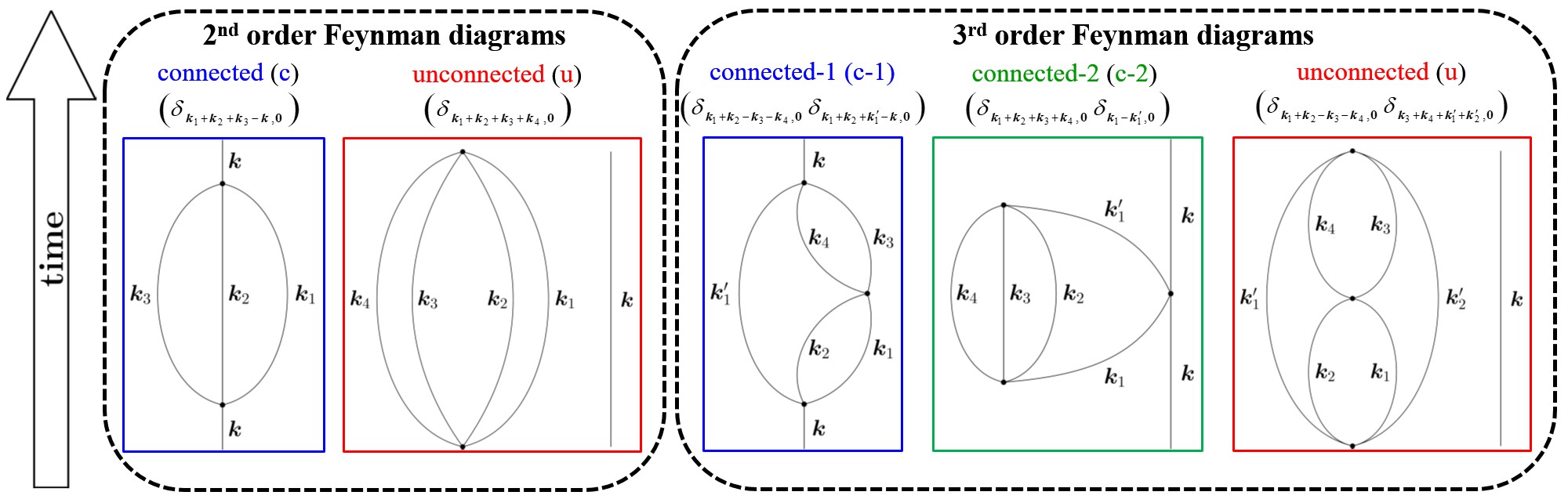
In this article in Physical Review D, doctoral student Panos Alatas and Vlasis Mavrantzas from our Department, jointly with Prof. Hans Christian Öttinger from ETH Zurich (https://polyphys.mat.ethz.ch/group/people/head.html) discuss the application of such an approach to the simplest possible quantum field theory, the so called phi^4 theory. Guided by a quantum master equation for the time evolution of such a system at zero temperature, they compute the corresponding Feynman diagrams contributing to the propagator of the scalar field up to third order in the interaction parameter, and analyze their topology. Next, they come up with a natural and quite elegant renormalization scheme, and finally they prove that this scheme beautifully recovers the critical coupling constant as a function of space dimensionality, already known from the more conventional Lagrangian approach to the same theory.
The work demonstrates the far-reaching, endless extensions of the concepts mastered by Chemical Engineering Students and how these can be used to provide unique solutions and fundamental insight into a variety of problems across all branches of natural sciences.
More details: https://journals.aps.org/prd/abstract/10.1103/PhysRevD.104.076007
| Attachment | Size |
|---|---|
| physrevd.104.076007.pdf | 565.71 KB |
